Illustration of the ideas behind Kernel Distributionally Robust Optimization
This project focuses on the mathematical optimization foundations of machine learning and control algorithms, and more broadly, data-driven algorithmic decision-making. We are especially motivated by addressing the lack of robustness and data distribution shift issues.
Our starting point is the standard sample average approximation (SAA), equivalent to empirical risk minimization (ERM). It optimizes the objective
$$ \min_\theta \frac1N\sum_{i=1}^N l(\theta, \xi_i), $$
where $l$ is the optimization objective, $\theta$ is the decision variable, and $\xi_i\sim P_0$ independent and identically distributed (i.i.d.) empirical data. ERM is the workhorse of modern machine learning. However, it is not suitable for safety-critical tasks since it does not guarantee generalization to new samples that do not come from $P_0$.
Instead of ERM, we explicitly robustify against data distribution shift using distributionally robust optimization (DRO)
$$\min_\theta \sup_{P\in \mathcal C}\mathbb E _{\xi\sim P} l(\theta, \xi),$$
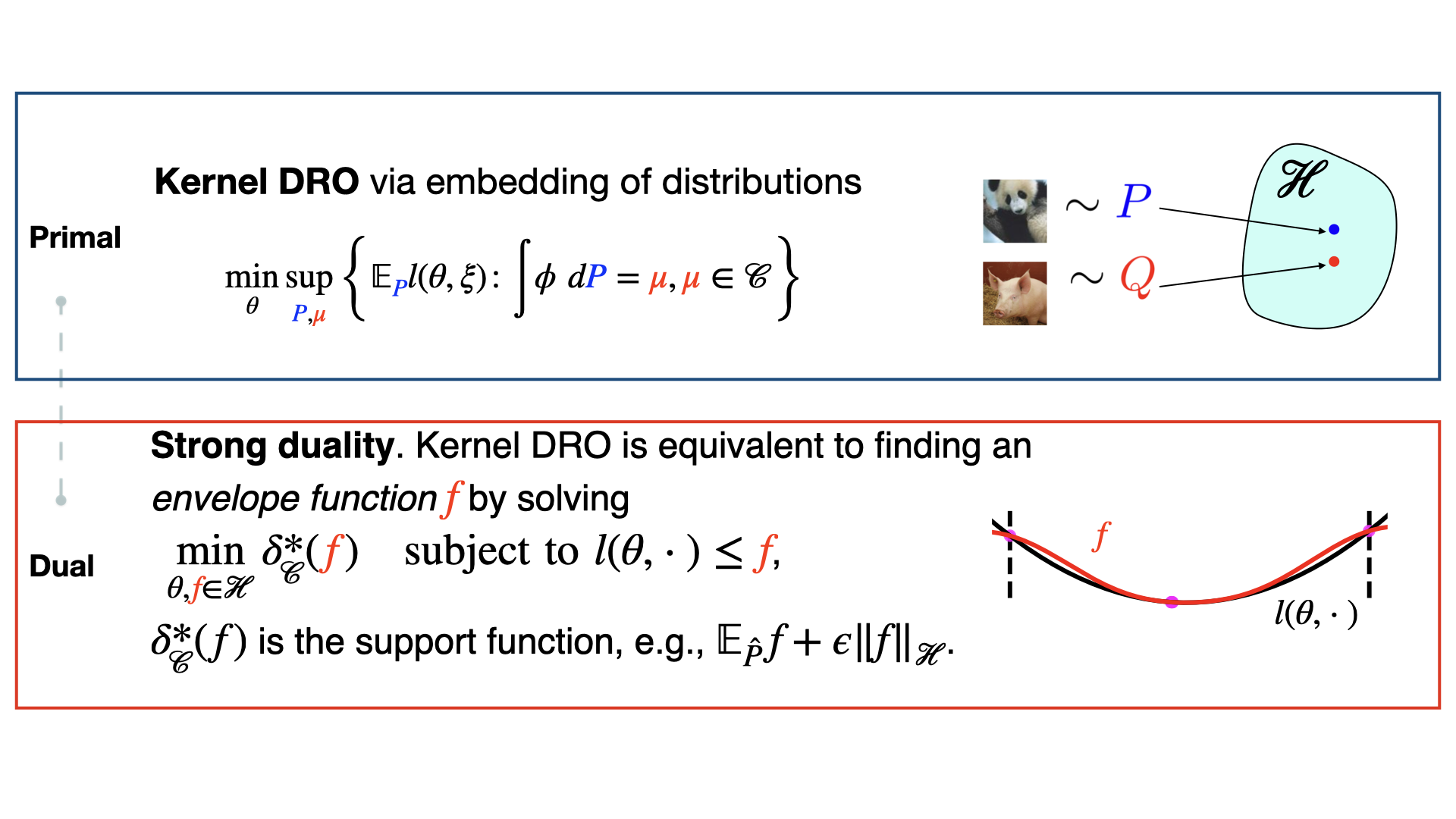
where $\mathcal C$ is a set of distributions, referred to as an uncertainty set. We established a kernel framework for DRO -- the Kernel DRO [ ], and show that the DRO problem can be exactly reformulated into a kernel learning problem. The intuition is to find a smooth kernel function that majorizes the original loss, as demonstrated in the illustration above.
The above work is closely related to and synergistic with our statistical learning projects. For example, we can use the aforementioned Kernel DRO algorithm constrained by an MMD uncertainty set
$$ \min_\theta \sup_{\operatorname{MMD}(P, \hat P_N)\leq\epsilon}\mathbb E _{\xi\sim P} l(\theta, \xi),$$
where the threshold $\epsilon$ can be chosen as a finite-sample error bound of our previous analyses [ ].
In addition to our focus on robust optimization, we also explore other optimization topics such as [ ].
