Predictive models enabled by modern machine learning methods can help address substantive questions in education, public policy, and social programs, but making reliable predictions in these domains requires accurate modeling of complex outcome distributions as well as accounting for unobserved confounders.
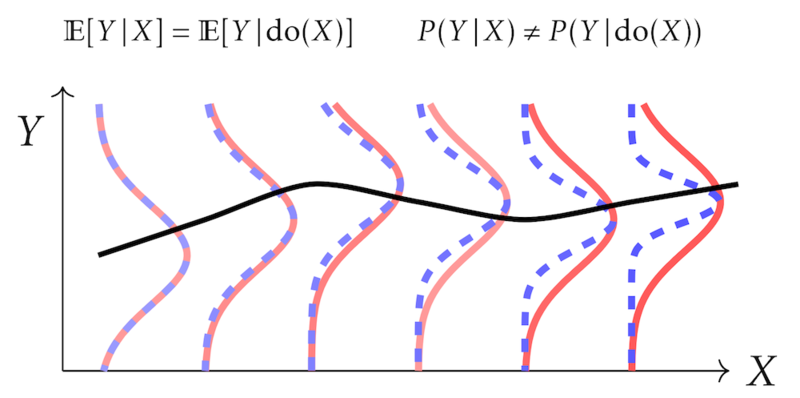
Figure: A comparison between the observational distribution $P(Y\,|\,X)$ (red solid line) and interventional distribution $P(Y \,|\, \text{do}(X))$ (blue dotted line) with the same conditional means, but different higher-order moments (conditional variances).
Distributional treatment effect To model complex outcome distributions, we proposed a \emph{counterfactual mean embedding} (CME) [ ] as a Hilbert space representation of the counterfactual distribution $P_{Y\langle 1|0 \rangle}(y) := \int P_{Y_1|X_1}(y\,|\,x)\, dP_{X_0}(x)$. The counterfactual $P_{Y\langle 1|0 \rangle}$ represents the outcome of hypothetical change which by definition is not observable, e.g., the birth weight of a baby had the mothers abstained from smoking. Without parametric assumptions, we proposed consistent estimators $\hat{\mu}_{Y\langle 1|0 \rangle}$ for the embedding $\mu_{Y\langle 1|0 \rangle}$ based on samples from the observable distributions $P_{X_0}$ and $P_{Y_1 X_1}$. We established consistency and convergence rate of $\hat{\mu}_{Y\langle 1|0 \rangle}$ which requires weaker assumptions than the previous work. Thanks to our estimators, the CME can be estimated consistently from observable quantities. One of the important applications of our work is offline policy evaluation, which is relevant to program evaluation in economics. In [ ], we extended this idea and proposed the \emph{conditional distributional treatment effect} (CoDiTE), which, in contrast to the more common CATE, is designed to encode a treatment's distributional aspects and heterogeneity beyond the mean. We then proposed estimating the CoDiTEs based on the maximum mean discrepancy (MMD) and U-statistics using kernel conditional mean embeddings and kernel ridge U-statistic regression, respectively.
Instrumental variables To account for unobserved confounders, we have developed ML-based methods for instrumental variable (IV) regression. Suppose that $X$ and $Y$ denote treatment and outcome variables, e.g., education and level of income, whose functional relationship can be described by $Y = f(X) + \varepsilon, \,\mathbb{E}[\varepsilon]=0$. The presence of unobserved confounders, e.g., socio-economic status, prevents us from learning $f$ with the standard nonparametric regression because $\mathbb{E}[\varepsilon\,|\,X] \neq 0$, i.e., $\mathbb{E}[Y\,|\,\text{do}(X)]\neq\mathbb{E}[Y\,|\,X]$. The idea of an instrumental variable (IV) regression is to leverage an instrument $Z$ that (i) induces a variation in $X$ (\emph{relevance}), (ii) affects $Y$ only through $X$ (\emph{exclusion restriction}), and (iii) is independent of the error term $\epsilon$ (\emph{exchangeability}). In this case, $f$ satisfies the Fredholm integral equation of the first kind: $\mathbb{E}[Y\,|\,Z] = \int f(X) \, dP(X|Z)$. Solving for $f$ is an ill-posed inverse problem. In [ ], we showed that this problem can be reformulated as a two-player game with a convex-concave utility function. When $\mathcal{F}$ and $\mathcal{U}$ are both RKHSes, the global equilibrium can be obtained in closed form. This reformulation also elucidates the kind of problems for which a game-theoretic perspective as a search for a Nash equilibrium can lead to simpler algorithms than the standard ones that solve the Fredholm integral equation directly. The work also sheds light on the duality between the two-stage and generalized method of moment-based approaches, as later pointed out in our work [ ] that applies the methods we develop to the setting of proximal causal learning.
